Symplectic Geometry
Geometric quantization of physics
A foreword about symplectic geometry. To keep it as simple as possible, Symplectic geometry is a branch of mathematics merging differential geometry and dynamical systems theory, based on the Hamiltonian formulation of classical mechanics. It is the study of manifolds with a symplectic form that allows to measure sizes. Indeed, in Riemannian geometry, the metric tensor gives lengths and angles, whereas the symplectic form measures areas. The term "symplectic" comes from the Greek word συμπλεκτικός (sumplektikós) meaning "intertwining" and was first coined by German mathematician Hermann Weyl in 1939, to replace the term "complex group" defining line complexes, in order to avoid the confusion with the more common definition of "complex", i.e. complex numbers.
Three mathematicians greatly developed symplectic geometry in the second half of the 20th century:



Based on the orbit method from Russian mathematician Alexandre Kirillov in representation theory, American mathematician Bertram Kostant and French mathematician Jean-Marie Souriau developed the modern theory of geometric quantization, which allows to make fundamental quantities of physics (like energy and momentum) emerge as pure geometrical objects.
Souriau (1922–2012) left a great legacy to mathematical physics in the fields of classical, relativistic and quantum mechanics. He notably introduced the important concepts of the moment space, the moment map (Hamiltonian action of a Lie group on a symplectic manifold, generalizing the notions of linear and angular momentum) and the coadjoint action, i.e. the action of a Lie group on the dual space to its Lie algebra. This allowed him, for instance, to give the first geometric and kinetic interpretations of spin. Below we're about to show that Souriau also gave a fundamental answer to the question: what is the real physical meaning for the reversal of time's arrow?
Gravity & T-symmetry
How time reversal means
energy and mass inversion
Lorentz transformations use space inversion and time reversal operators, which can provoke \(\text{P}\)-symmetry, \(\text{T}\)-symmetry, or \(\text{PT}\)-symmetry. The Lorentz group has therefore four connected components:
- • two orthochronous transformations (motions going forward in time),
- • two antichronous transformations (motions going backward in time).
They will be more detailed thereafter.
In classical mechanics, the antichronous transformations, which revert time with \(\text{T}\)-symmetry and \(\text{PT}\)-symmetry, are dismissed as being "unphysical", so only half of the Lorentz and Poincaré groups are used: the restricted Lorentz group and the restricted Poincaré group, which use only the orthochronous transformations.
But in 1970, Souriau used a non-trivial extension of the full Poincaré group to show the real physical meaning of time reversal for a particle: \(\text{T}\)-symmetry equals energy inversion. If a particle has a nonzero inertial mass, it means that if the energy of that particle is inverted, so is its mass (since \(m = E / c^2\)), that is to say: Time reversal produces negative mass. Souriau's 1970 book on symplectic geometry (a must in the field), which contains that important demonstration with more details in chapter 14, has been translated in English in 1997. 8 |
Dynamical
group theory
Lie groups and their Lie algebra
What is group theory? What are "groups"? Mathematically, we'll see they are simply some matrices acting on other matrices. But physically, what are they?

What is a group?
- • A group is made to transport.
- • The way we transport is more important than what is being transported.
Tell me how you move, I'll tell you what you are.
— Jean-Marie Souriau —
All groups exposed herein are Lie groups. They are assembled together to form other groups:
The Orthogonal group \(\text{O(3)}\) is the fundamental group which preserves distances in transformations in a Euclidean space, managing rotations and symmetries in 3D. It contains the important subgroup \(\text{SO(3)}\) (Special Orthogonal 3D) also called the rotation group because it is the one which manages rotations around an axis (as for \( \text{SO(2)} \), special orthogonal group in two dimensions, it handles rotations around a point).
The Euclidean group \(\text{E(3)}\) is an isometry group of the 3D Euclidean space, where it manages rotations, symmetries and translations. It is made on top of the group \(\text{O(3)}\). To put it very simply, it is a static group, a group of the intemporal space. Physically, it can be decomposed into a force and a couple applied on the object of study in rigid body mechanics.
These sets of actions on objects in space by such groups conserve lengths. These groups and their subgroups can position an object in space, rotate it around a point or a line, but also make it become its image in a mirror (\(\text{P}\)-symmetry).
According to Einstein's special relativity, instead of living in a 3D Euclidean space \({[x,y,z]}\) of signature \((+++)\) where time is a separate entity, we are actually living in a 4D hypersurface where the three dimensions of space are perpendicular to a dimension of time, in a single spacetime \({[t,x,y,z]}\) called a Minkowski space, of signature \((-+++)\).
Similarly, the Euclidean group (where time is absent) generates static objects which populate their associated space. When time enters the picture (which Souriau associates to its own group of time translations, the Chronos group), group theory becomes dynamical group theory, which no longer manages static objects, but sets of "event-points" or trajectories.
The Galilei group (or Galilean group) \(\text{Gal(3)}\) manages motions of the non-relativistic material point, i.e. classical mechanics. Souriau decomposes the Galilei group in two subgroups:
- • Euclidean transformatons + time translations = Aristotle group, a 10-dimension group.
- • The Bruno group (named after the famous Italian Dominican friar, philosopher, mathematician, poet, and cosmological theorist Giordano Bruno, proponent of Copernicus' heliocentric model and partisan of the plurality of worlds in an infinite universe with no center. He was tried for heresy by the Roman Inquisition and sentenced to death by burning alive). Souriau says that the Bruno group "embarks", in reference to someone embarking aboard "Bruno's boat" moving on a river.
The Aristotle group is a dogmatic group, as its name suggests. It could produce an impression of immobility, as someone sleeping in his armchair at home, for example. But the same person also moves at a great velocity around the Sun, which itself moves at an even greater velocity around the galaxy… Stillness is therefore only a subjective regularity: it depends on the chosen frame of reference. Fortunately, a more objective geometry can be achieved by another group. To do this, let's go back to Bruno: the trajectory of a stone thrown in the air can be obtained from both the shore or from the boat. The motion which, as seen from the boat, would become exactly the same as the actual motion seen from the shore, would be another possible motion. The embarkation thus becomes a correspondence between motions at the same instant, which Souriau calls the Bruno transformations.
As from the Galilei group, it can be obtained by completing the Aristotle group with "Galilei transformations", i.e. adding the same initial velocity to all points of the system. The application of Noether's symplectic theorem then predicts that the motion of the center of mass is uniform and occurs in a straight line, a result sometimes known as the principle of inertia (first formulated by French mathematician Pierre Gassendi in 1642). To establish the same result with his first law of motion, Isaac Newton had to introduce a special principle of mechanics, the equality of action and reaction. But in symplectic geometry, Newton's third law is useless: the Galilean symplectic invariance alone is sufficient.
Every action of the Galilei group can be decomposed into two actions, one taken in the Aristotle group and the other in the Bruno group.

Dismantling the Poincaré group
On the hunt for its invariants
As seen above, the Galilei group secretes the laws of classical Newtonian mechanics. Another group is compatible with special relativity: the Poincaré group, a ten-dimensional Lie group, that of Minkowski spacetime isometries.
The Poincaré group thus manages motions of the relativistic material point in a 4D spacetime. Geometric quantization allows for example to retrieve the non-relativistic (free) Schrödinger equation from the Galilei group presented above, and the Klein-Gordon equation from the Poincaré group, which is the group we will focus on in the following.
In early 20th century, great German mathematician Emmy Noether gave her name to one of the most important theorems of physics: Noether's theorem, which states that for every subgroup of a dynamical group, corresponds an invariant.
In the Poincaré group, there is a first subgroup of time translations:
$$ \begin{bmatrix} 1 & 0 & 0 & 0 & \Delta t \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} t \\ x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} t + \Delta t\\ x \\ y \\ z \\ 1 \end{bmatrix} $$
It is a group with one parameter (\(\Delta t\)), and its corresponding invariant is a scalar :
The energy \(E\).
s has also a second subgroup of spatial translations:
$$ \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & \Delta x \\ 0 & 0 & 1 & 0 & \Delta y \\ 0 & 0 & 0 & 1 & \Delta z \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} t \\ x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} t \\ x + \Delta x \\ y + \Delta y \\ z + \Delta z \\ 1 \end{bmatrix} $$
which is a group with three parameters (\(\Delta x, \Delta y, \Delta z\)). Its invariant is the (linear) momentum:
$$ \text{p} = \begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix} $$
This is how momentum is defined according to dynamical group theory. Such geometric quantization makes fundamental quantities of physics become pure geometrical objects.
Similarly to the two previous subgroups of the Poincaré group, we can make a third act, the subgroup of spacetime translations:
$$ \begin{bmatrix} 1 & 0 & 0 & 0 & \Delta t \\ 0 & 1 & 0 & 0 & \Delta x \\ 0 & 0 & 1 & 0 & \Delta y \\ 0 & 0 & 0 & 1 & \Delta z \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} t \\ x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} t + \Delta t \\ x + \Delta x \\ y + \Delta y \\ z + \Delta z \\ 1 \end{bmatrix} $$
The invariant object would then be the energy-momentum four-vector or four-momentum:
$$ \text{P} = \begin{bmatrix} E \\ p_x \\ p_y \\ p_z \end{bmatrix} $$
We've just seen 4 parameters (or dimensions, beware such "dimensions" of a group are just a math terminology) of the Poincaré group, which contains 10 dimensions. What are these other 6 parameters? They are the dimensions of the Lorentz group \(\text{L}\), which is a subgroup of the Poincaré group:
$$ \begin{bmatrix} \text{L} & 0 \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} \xi \\ 1 \end{bmatrix} = \begin{bmatrix} \text{L} \, \xi \\ 1 \end{bmatrix} \qquad \text{with} \qquad \xi = \begin{bmatrix} t \\ x \\ y \\ z \end{bmatrix} $$
Noether's theorem says it must have a corresponding "object" in physics, defined by 6 parameters that are invariant under the action of this subgroup.
Souriau showed that such object contains the spin, and that it has a dimension of angular momentum.
The "moment"
The shadow of every move
We've seen that the subgroups above correspond somewhat to a kind of "dismantling the group, part by part". When we do the opposite operation, we reconstitute the group. The set of invariants shown above constitutes what Souriau calls the moment \(\text{J}\):
$$ \text{J} \, = \, \left\{ E, p_x, p_y, p_z, ..., \text{spin} \right\} $$
Every movement of an object in spacetime has its moment. Beware, such "moment" is not a synonym of "instant", nor of the physical concepts of linear or angular momentum. The word "moment" used since 1765 (it was introduced by Swiss mathematican Leonhard Euler), is related to movimentum in Latin, which means movement, i.e. a physical motion between points in space. There is a tight and fundamental relationship between "motion" and "moment".
The moment, symbol of materiality, shadows every move.
The Moment Space
A geometry can hide another
A group action is how a group of matrices can act through their multiplication in a way to manage, for example in the Euclidean group, rotations, symmetries and translations in one fell swoop.
But Souriau discovered that a group can also act on moments, generating in return a new geometric space. As a consequence, there exist another action of the group on ANOTHER SPACE. There is indeed one space where motions are inscribed: spacetime. In Minkowski 4D spacetime, a group acts on a point \( \left\{ t_1, x_1, y_1, z_1 \right\} \) which gives another point \( \left\{ t_2, x_2, y_2, z_2 \right\} \). However, what is inscribed in spacetime is only the trajectory. Yet, the motion plays in two spaces, the second one being the space of the parameters of the motion, which Souriau calls the moment space.
Let's consider a motion of an object in space. Such motion is also defined by its moment \(\text{J}\). The physicist can then make an element \(g\) of say, the Galilei group, act on this moment \(\text{J}\). He obtains a new motion, hence a new moment \(\text{J}'\). This action is written:
$$ \text{J}' \, = \, g \times \text{J} \times {}^\text{t}\kern{-2pt}g $$
\(g\) is the element of the chosen group, a square matrix, which is simply a matrix with the same number of lines and columns, e.g.:
\({}^\text{t}\kern{-1pt}g\) is the transpose of that matrix, i.e. the symmetric inverse of the square table with respect to its main diagonal:

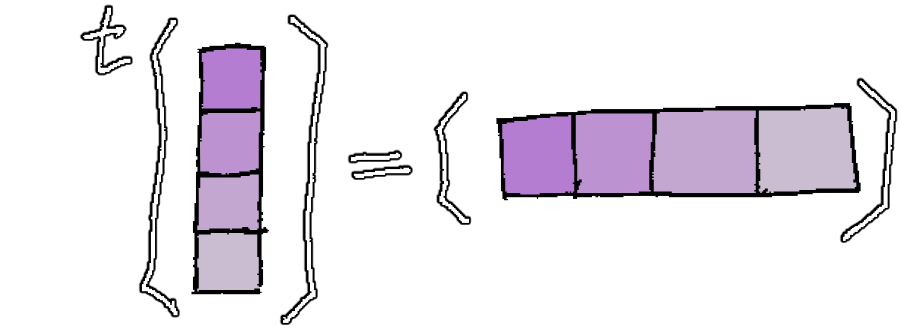
And for the special case of a column vector, its transpose is simply the same matrix written as as a row vector:
\(\text{J}\) is the moment matrix. It is a 5×5 antisymmetric matrix, i.e the symmetric elements with respect to the main diagonal have opposite signs. The elements of the main diagonal are equal to zero (which is its own opposite). We can count the components of such antisymmetric matrices:
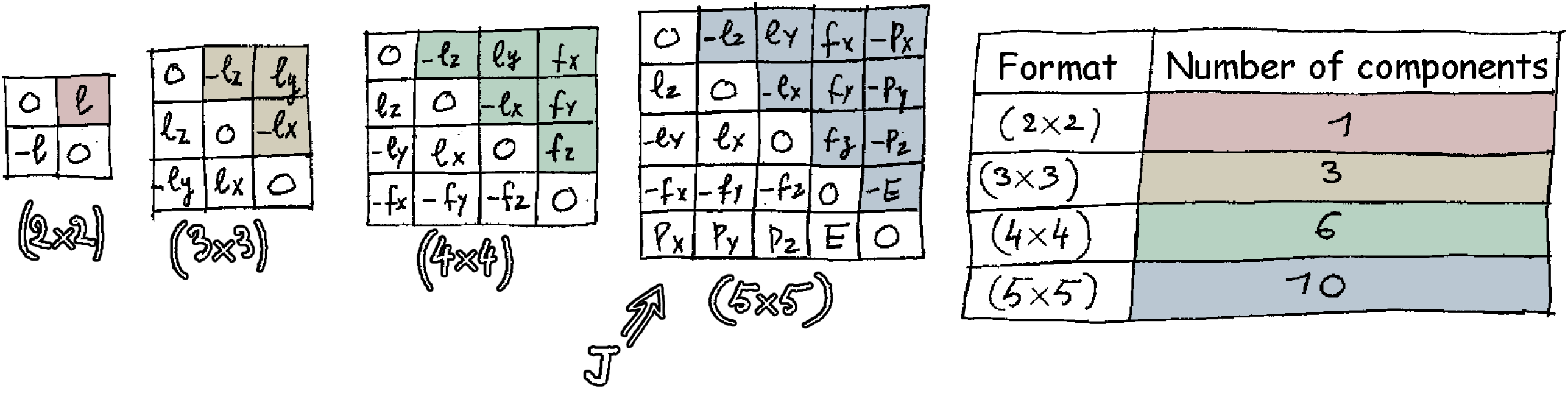
To better understand what \(\text{J}\) is, that 5×5 matrix can be decomposed in the 4×4 matrix \( \color{#b7d2c2}{\text{M}} \), the energy-momentum four-vector \( \color{#a07dd1}{\text{P}} \) (column vector with four components) and its transpose the row vector \( \color{#cabcd1}{{}^\text{t}\kern{-1pt}\text{P}} \):
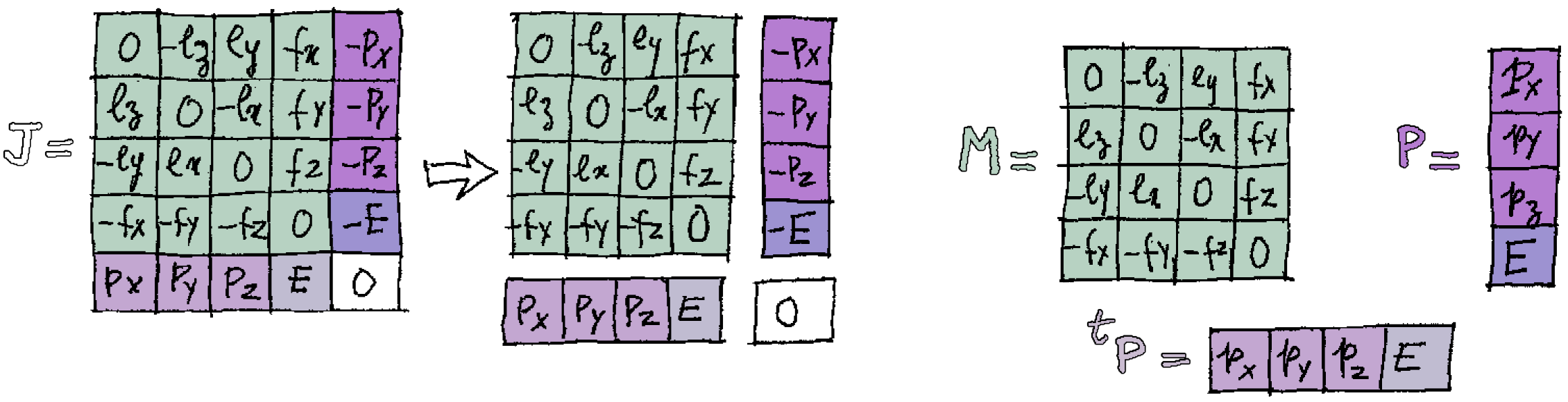
We can now write the moment matrix \(\text{J}\) in a more compact way:
$$ \text{J} = \begin{bmatrix} \color{#b7d2c2}{\text{M}} & \color{#a07dd1}{-\text{P}} \\ \color{#cabcd1}{{}^\text{t}\kern{-1pt}\text{P}} & 0 \end{bmatrix} $$
We've shown that the moment-matrix \(\text{J}\) contains objects that have a physical interpretation, like the four-vector \( \color{#a07dd1}{\text{P}} \), in which \( \color{#9d92d1}{E} \) is the energy and \( \color{#b57dd1}{\text{p} = \left\{ p_x, p_y, p_z \right\} } \) the momentum. But what is exactly that antisymmetric matrix \( \color{#b7d2c2}{\text{M}} \)? What is its physical meaning? Let's decompose it to find out:
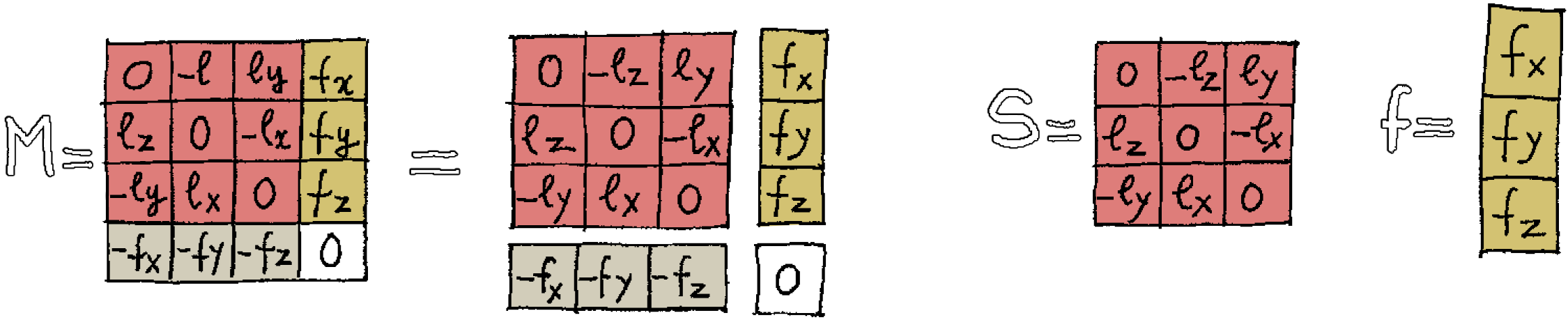
In the compact form:
$$ \color{#b7d2c2}{\text{M}} = \begin{bmatrix} \color{#d1827d}{\text{s}} & \color{#d1c27d}{\text{f}} \\ \color{#d1cdbc}{-{}^\text{t}\kern{-1pt}\text{f}} & 0 \end{bmatrix} $$
The velocity \(V\) is implicitly present in the \( \text{L} \) matrix of the Lorentz group. If we consider a motion occurring in a specific direction, for example along a vector \(oz\), with a velocity \(V\) and a translation \(\Delta z = \text{c}\), and if \(\text{c} = V \, \Delta t\), then we are in a coordinate system where we follow the particle's motion along this spacetime translation. The vector \( \color{#d1c27d}{ \text{f} } \) is then shown to be null.
The matrix \( \color{#d1827d}{ \text{s} } \) is then written:
$$ \color{#d1827d}{ \text{s} = \begin{bmatrix} 0 & -s & 0 \\ s & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} } $$
It is the spin of the particle. Souriau demonstrated in 1970 this purely geometric character of spin: a 3×3 antisymmetric matrix. 8 The method of geometric quantization, which he invented, allows to show that spin can only be a multiple of a fixed quantity: \(\hbar\) (the reduced Planck constant).
Further down the page, we will see that Souriau also showed that a particle with an electric charge is equivalent of saying that it moves in a spacetime having a fifth dimension (similar to the Kaluza or Jordan–Thiry dimension), and that such dimension is really tiny (its characteristic length is the Planck length) and is closed onto itself as a fiber bundle. It is the fact that this dimension is closed onto itself that causes the electric charge to be quantized. In spacetime, there exists a "form of closure" that causes an object to become identical to itself under the action of a 360° rotation. The quantization of spin comes from that property: there is a close relationship between geometric quantization and the closure of a dimension.
The quantity
$$ \color{#d1c27d}{ \text{f} = \begin{bmatrix} f_x \\ f_y \\ f_z \end{bmatrix} } $$
is what Souriau calls the passage. It vanishes when the frame of reference is that of the particle in motion, and appears only from another reference frame, for exemple considering an object spinning on a moving boat from the shore. It may be considered as an artifact of the motion, although Souriau said about it:

What is the passage?
It is what prevents you from moving without moving something in the opposite direction: the exchange of passage between this thing and you.
Proof that it is real: by plane or by boat, there is a toll per passage.
— Jean-Marie Souriau —
For example, you are sitting in a plane in flight at the rear of the cabin, and you are invited to move to the front. You will only pass if you borrow a little passage from the aircraft. This will cause it to lose a couple of inches off of its flight plan. It is the conservation of passage that makes it possible to establish the following rule: if an object is in free space, its center of mass moves in a straight line, at a constant speed, in the direction of the momentum. If the momentum is equal to zero, the center of mass is immobile. Of course, in reality a rocket launched in space is not completely free, it undergoes the gravitational attraction of planetary bodies and the Sun, which slowly disrupt the motion of the center of gravity by transferring some passage to the rocket.
The underlying quantity here is more classical than the passage \( \color{#d1c27d}{\text{f}} \): it is the center of mass \( C_m \). They are deduced from each other by the rule \( C_m = \color{#d1c27d}{\text{f}} + \color{#b57dd1}{p} \, t \). Therefore the passage \( \color{#d1c27d}{\text{f}} \) locates the position of \( C_m \) at the instant \( t = 0 \).
The complete Galilean moment is thus:
$$ \text{J} \, = \, \left\{ \text{energy, mass, momentum, passage, spin} \right\} $$
Every motion of any thing has its own moment, and the only thing a moment can do is to transfer itself partially from one thing to another. It cannot be created nor disappear. This is how the moment can be measured, by taking a part of the moment of the object, and transferring it to the measuring instrument.
You see above that (rest) mass is a parameter of the moment. The classical mass, which arose as an arbitrary additive constant in the Galilei group, is now defined in the Poincaré group as the relativistic mass \( m = E / c^2 \) which depends on velocity. Another difference with the non-relativistic dynamical group: there is no barycentric decomposition anymore. It was a consequence in the Galilei group of the existence of a privileged subgroup which does not have an equivalent in the Poincaré group. Then, every virtual motion can be derived from the real motion with a change of reference frame, and it is shown that the Poincaré group describes properties of elementary particles using only two numbers which have a physical interpretation: the rest mass and spin (i.e. intrinsic angular momentum).
For the case of a massless particle (like the photon), a third number steps in: the helicity (circular dichroism), which can take only the values ±1. Photons are indeed either left circularly polarized (LCP) or right circularly polarized (RCP) according to the sign of the helicity.
Now that we have exposed the main tools, we can show the coaction of the Poincaré group on its moment space.
Coadjoint action
Action of the Poincaré group
on its moment space
The coadjoint action is the action of a group on its moment space, in more mathematical terms, it is the action of a Lie group on the dual vector space to its Lie algebra, or Lie coalgebra.
In dynamical systems theory, The Poincaré group manages the motion of the relativistic material point. The element \(g\) of the Poincaré group is:
$$ g = \begin{bmatrix} \text{L} & \text{C} \\ 0 & 1 \end{bmatrix} $$
where \(\text{L}\) is the Lorentz group (subgroup of the Poincaré group) and \(\text{C}\) is a column vector representing a translation within four dimensions:
$$ \text{C} = \begin{bmatrix} \Delta t \\ \Delta x \\ \Delta y \\ \Delta z \\ \end{bmatrix} $$
Thanks to the decomposition of the previous section, we can detail the action of the Poincaré group on its moment space, which is:
$$ \text{J}' \, = \, g \times \text{J} \times {}^\text{t}\kern{-2pt}g $$
We have:
$$ {}^\text{t}\kern{-1pt}g \, = \, \begin{bmatrix} {}^\text{t}\kern{-1pt}\text{L} & 0 \\ {}^\text{t}\kern{-1pt}\text{C} & 1 \end{bmatrix} $$
Expanding the compact notation of the action above, we have:
$$ \begin{aligned} \text{J}' \, &= \, \begin{bmatrix} \text{L} & \text{C} \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} \text{M} & -\text{P} \\ {}^\text{t}\kern{-1pt}\text{P} & 0 \end{bmatrix} \times \begin{bmatrix} {}^\text{t}\kern{-1pt}\text{L} & 0 \\ {}^\text{t}\kern{-1pt}\text{C} & 1 \end{bmatrix} \\ \text{J}' \, &= \, \begin{bmatrix} \text{L} & \text{C} \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} \text{M} \, {}^\text{t}\kern{-1pt}\text{L} - \text{P} \, {}^\text{t}\kern{-1pt}\text{C} & -\text{P} \\ {}^\text{t}\kern{-1pt}\text{P} \, {}^\text{t}\kern{-1pt}\text{L} & 0 \end{bmatrix} \\ \text{J}' \, &= \, \begin{bmatrix} \color{#b7d2c2}{ \text{L} \, \text{M} \, {}^\text{t}\kern{-1pt}\text{L} - \text{L} \, \text{P} \, {}^\text{t}\kern{-1pt}\text{C} + \text{C} \, {}^\text{t}\kern{-1pt}\text{P} \, {}^\text{t}\kern{-1pt}\text{L} } & \color{#a07dd1}{ -\text{L} \, \text{P} } \\ \color{#cabcd1}{ {}^\text{t}\kern{-1pt}\text{P} \, {}^\text{t}\kern{-1pt}\text{L} } & 0 \end{bmatrix} \end{aligned} $$
Since:
$$ \text{J} = \begin{bmatrix} \color{#b7d2c2}{\text{M}} & \color{#a07dd1}{-\text{P}} \\ \color{#cabcd1}{{}^\text{t}\kern{-1pt}\text{P}} & 0 \end{bmatrix} $$
We have:
$$ \color{#b7d2c2}{\text{M}' \, = \, \text{L} \, \text{M} \; {}^\text{t}\kern{-1pt}\text{L} - \text{L} \, \text{P} \; {}^\text{t}\kern{-1pt}\text{C} + \text{C} \, {}^\text{t}\kern{-1pt}\text{P} \, {}^\text{t}\kern{-1pt}\text{L}} $$
$$ \color{#a07dd1}{ \text{P}' \, = \, \text{L} \, \text{P} } $$
This is the coadjoint action of the Poincaré group on its moments \(\color{#b7d2c2}{\text{M}}\) (passage and spin) and \(\color{#a07dd1}{\text{P}}\) (energy and momentum).
Antichronous action
how energy is reversed
The elements of the Lorentz group act on a series of points in spacetime which constitute a motion. By letting an element \(\text{L}\) of the Lorentz group act on a given motion, we obtain another motion.
The full Lorentz group has four connected components:
\(\text{L}_\text{N}\) (neutral), \(\text{L}_\text{P}\) (inverts space), \(\text{L}_\text{T}\) (inverts time), \(\text{L}_{\text{PT}}\) (inverts space and time).
The neutral component \(\text{L}_\text{N}\) is a subgroup containing the unitary matrix that does not invert space nor time. Then, we introduce Petit's writing, which consists in the following 4-element matrix \(\omega\) built with two parameters \( \color{#7da9d1}{\lambda_1} \) and \( \color{#bcc7d1}{\lambda_2} \):
$$ \omega_{(\color{#7da9d1}{\lambda_1}, \, \color{#bcc7d1}{\lambda_2})} = \begin{bmatrix} \color{#7da9d1}{\lambda_1} & 0 & 0 & 0 \\ 0 & \color{#bcc7d1}{\lambda_2} & 0 & 0 \\ 0 & 0 & \color{#bcc7d1}{\lambda_2} & 0 \\ 0 & 0 & 0 & \color{#bcc7d1}{\lambda_2} \\ \end{bmatrix} \qquad \text{with} \qquad \begin{matrix} \color{#7da9d1}{\lambda_1 = \pm 1} \\ \color{#bcc7d1}{\lambda_2 = \pm 1} \end{matrix} $$
Thus the four components of the full Lorentz group can easily be expressed using the four possible combinations of these two parameters applied on the neutral component \(\text{L}_\text{N}\):
$$ \text{L} \; = \; \omega \, \text{L}_{\text{N}} $$
Indeed, we have:
| \( \omega_{(\color{#7da9d1}{1}; \, \color{#bcc7d1}{1})} \times \text{L}_\text{N} = \begin{bmatrix} \color{#7da9d1}{1} & 0 & 0 & 0 \\ 0 & \color{#bcc7d1}{1} & 0 & 0 \\ 0 & 0 & \color{#bcc7d1}{1} & 0 \\ 0 & 0 & 0 & \color{#bcc7d1}{1} \end{bmatrix} \in \left\{ \text{L}_\text{N} \right\} \) | \( \omega_{(\color{#7da9d1}{1}; \, \color{#bcc7d1}{-1})} \times \text{L}_\text{N} = \begin{bmatrix} \color{#7da9d1}{1} & 0 & 0 & 0 \\ 0 & \color{#bcc7d1}{-1} & 0 & 0 \\ 0 & 0 & \color{#bcc7d1}{-1} & 0 \\ 0 & 0 & 0 & \color{#bcc7d1}{-1} \end{bmatrix} \in \left\{ \text{L}_\text{P} \right\} \) |
| \( \omega_{(\color{#7da9d1}{-1}; \, \color{#bcc7d1}{1})} \times \text{L}_\text{N} = \begin{bmatrix} \color{#7da9d1}{-1} & 0 & 0 & 0 \\ 0 & \color{#bcc7d1}{1} & 0 & 0 \\ 0 & 0 & \color{#bcc7d1}{1} & 0 \\ 0 & 0 & 0 & \color{#bcc7d1}{1} \end{bmatrix} \in \left\{ \text{L}_\text{T} \right\} \) | \( \omega_{(\color{#7da9d1}{-1}; \, \color{#bcc7d1}{-1})} \times \text{L}_\text{N} = \begin{bmatrix} \color{#7da9d1}{-1} & 0 & 0 & 0 \\ 0 & \color{#bcc7d1}{-1} & 0 & 0 \\ 0 & 0 & \color{#bcc7d1}{-1} & 0 \\ 0 & 0 & 0 & \color{#bcc7d1}{-1} \end{bmatrix} \in \left\{ \text{L}_{\text{PT}} \right\} \) |
We see that \(\color{#7da9d1}{\lambda_1 = -1}\) inverts time and \(\color{#bcc7d1}{\lambda_2 = -1}\) inverts space. The four sets are grouped in two subsets: the orthochronous subset \(\text{L}_\text{O}\) and the antichronous subset \(\text{L}_\text{A}\):
$$ \color{#04c4fc}{\text{L}_\text{O} \, = \, \left\{ \text{L}_\text{N} ; \text{L}_\text{P} \right\}} \qquad \text{and} \qquad \color{#04c4fc}{\text{L}_\text{A} \, = \, \left\{ \text{L}_\text{T} ; \text{L}_{\text{PT}} \right\}} $$
The full Poincaré group, built on top of the Lorentz group adding spacetime translations, has also these four connected components. Thus its element can be written:
$$ g = \begin{bmatrix} \omega \, \text{L}_{\text{N}} & \text{C} \\ 0 & 1 \end{bmatrix} $$
Then the action of the Poincaré group on spacetime, the space of trajectories, is:
$$ \begin{bmatrix} \omega \, \text{L}_{\text{N}} & \text{C} \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} \xi \\ 1 \end{bmatrix} = \begin{bmatrix} \omega \, \text{L}_{\text{N}} \, \xi + \text{C} \\ 1 \end{bmatrix} $$
But this action hides a more important action: the action of the Poincaré group on its moment \(\text{J}\), which has ten scalars (since the Poincaré group is a 10-dimensional group), these scalars being:
- • The energy \( \color{#9d92d1}{E} \)
- • The momentum \( \color{#b57dd1}{ \text{p} = \left\{ p_x, p_y, p_z \right\} } \)
- • The passage \( \color{#d1c27d}{ \text{f} = \left\{ f_x, f_y, f_z \right\} } \)
- • The spin \( \color{#d1827d}{ \text{s} = \left\{ l_x, l_y, l_z \right\} } \)
The dual of the action of the Poincaré group on its Lie algebra is the coadjoint action on its moments \(\color{#b7d2c2}{\text{M}}\) (passage and spin) and the four-momentum vector \(\color{#a07dd1}{\text{P}}\) (energy and momentum) which gives in this case, following the writing seen previously:
$$ \color{#b7d2c2}{\text{M}' \; = \; (\omega\text{L}_{\text{N}}) \, \text{M} \; {}^\text{t}\kern{-1pt}(\omega\text{L}_{\text{N}}) \; - \; (\omega\text{L}_{\text{N}}) \, \text{P} \; {}^\text{t}\kern{-1pt}\text{C} \; + \; \text{C} \, {}^\text{t}\kern{-1pt}\text{P} \, {}^\text{t}\kern{-1pt}(\omega\text{L}_{\text{N}}) } $$
$$ \color{#a07dd1}{ \text{P}' \; = \; (\omega\text{L}_{\text{N}}) \, \text{P} } $$
To highlight the effects of \(\text{P}\), \(\text{T}\) and \(\text{PT}\) symmetries on \( \left\{ \color{#9d92d1}{E}, \color{#b57dd1}{\text{p}}, \color{#d1c27d}{\text{f}}, \color{#d1827d}{\text{s}} \right\} \), we will choose the simplest possible action, where there is no spacetime translation, so the vector \(\text{C}\) cancels out. We also simplify the writing, choosing \(\text{L}_{\text{N}} = 1 \). We get:
$$ \color{#b7d2c2}{ \text{M}' \; = \; \big[ \omega_{(\lambda_2, \, \lambda_1)} \big] \times \text{M} \times {}^\text{t}\kern{-1pt}\big[ \omega_{(\lambda_2, \, \lambda_1)} \big] } $$
$$ \color{#a07dd1}{ \text{P}' \; = \; \big[ \omega_{(\lambda_2, \, \lambda_1)} \big] \, \text{P} } $$
Let's consider for example \(\text{T}\)-symmetry, where there is only time inversion ( \( \color{#7da9d1}{\lambda_1 = -1}\) ), no space inversion ( \( \color{#bcc7d1}{\lambda_2 = 1} \) ), in a case where there is also no spacetime translation ( \( \text{C}=0 \) ). We thus have:
$$ \omega_{(\color{#bcc7d1}{1}, \, \color{#7da9d1}{-1})} \times \text{L}_{\text{N}} \; \equiv \; \text{L}_{\text{T}} $$
Hence:
$$ \text{L}_{\text{T}} \times \xi \; = \; \begin{bmatrix} \color{#bcc7d1}{1} & 0 & 0 & 0 \\ 0 & \color{#bcc7d1}{1} & 0 & 0 \\ 0 & 0 & \color{#bcc7d1}{1} & 0 \\ 0 & 0 & 0 & \color{#7da9d1}{-1} \end{bmatrix} \times \begin{bmatrix} x \\ y \\ z \\ t \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \\ -t \end{bmatrix} $$
This is the trivial action of time reversal in the space of trajectories. But the coadjoint action, the action of the group on its moment space, gives on one hand:
\[ \begin{aligned} \color{#b7d2c2}{ \text{M}' \, = \, \text{L}_\text{T} \times \text{M} \times {}^\text{t}\kern{-1pt}\text{L}_\text{T} } \, &= \, \begin{bmatrix} \color{#bcc7d1}{1} & 0 & 0 & 0 \\ 0 & \color{#bcc7d1}{1} & 0 & 0 \\ 0 & 0 & \color{#bcc7d1}{1} & 0 \\ 0 & 0 & 0 & \color{#7da9d1}{-1} \end{bmatrix} \times \begin{bmatrix} \color{#d1827d}{0} & \color{#d1827d}{-l_z} & \color{#d1827d}{l_y} & \color{#d1c27d}{f_x} \\ \color{#d1827d}{l_z} & \color{#d1827d}{0} & \color{#d1827d}{-lx} & \color{#d1c27d}{f_y} \\ \color{#d1827d}{-l_y} & \color{#d1827d}{l_x} & \color{#d1827d}{0} & \color{#d1c27d}{f_z} \\ \color{#d1cdbc}{-f_x} & \color{#d1cdbc}{-f_y} & \color{#d1cdbc}{-f_z} & 0 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{bmatrix} \\ \color{#b7d2c2}{ \text{M}' } \, &= \, \begin{bmatrix} \color{#d1827d}{0} & \color{#d1827d}{-l_z} & \color{#d1827d}{l_y} & \color{#d1c27d}{-f_x} \\ \color{#d1827d}{l_z} & \color{#d1827d}{0} & \color{#d1827d}{-lx} & \color{#d1c27d}{-f_y} \\ \color{#d1827d}{-l_y} & \color{#d1827d}{l_x} & \color{#d1827d}{0} & \color{#d1c27d}{-f_z} \\ \color{#d1cdbc}{f_x} & \color{#d1cdbc}{f_y} & \color{#d1cdbc}{f_z} & 0 \end{bmatrix} \end{aligned} \]
and on the other hand:
$$ \color{#a07dd1}{ \text{P}' \; = \; \text{L}_\text{T} \times \text{P} } \; = \; \begin{bmatrix} \color{#bcc7d1}{1} & 0 & 0 & 0 \\ 0 & \color{#bcc7d1}{1} & 0 & 0 \\ 0 & 0 & \color{#bcc7d1}{1} & 0 \\ 0 & 0 & 0 & \color{#7da9d1}{-1} \end{bmatrix} \times \begin{bmatrix} \color{#b57dd1}{p_x \\ p_y \\ p_z} \\ \color{#9d92d1}{E} \end{bmatrix} = \begin{bmatrix} \color{#b57dd1}{p_x \\ p_y \\ p_z} \\ \color{#9d92d1}{-E} \end{bmatrix} $$
N.B.: The matrix \(\omega_{(\color{#bcc7d1}{\lambda_2}, \; \color{#7da9d1}{\lambda_1})}\) is here expressed according to a 4D spacetime noted \( \left\{ x, y, z, t \right\} \) instead of the usual relativity convention \( \left\{ t, x, y, z \right\} \) that we use everywhere else, in order to fit with the graphical and matrix representations of \( \color{#b7d2c2}{ \text{M} } \) and \( \color{#a07dd1}{ \text{P} } \) as shown earlier.
We can detail the same process for the 4 connected components of the Lorentz group and we discover that:
- • P-symmetry: momentum and passage are inverted. Energy and spin stay the same.
- • T-symmetry: energy and passage are inverted. Momentum and spin stay the same.
- • PT-symmetry: momentum and energy are inverted. Passage and spin stay the same.
The following table details the possibles Lorentz transformations and their effect on the moment components.
| $$ \text{N} $$ | $$ \text{P} $$ | $$ \text{T} $$ | $$ \text{PT} $$ | ||
|---|---|---|---|---|---|
| $$ \lambda_2 = 1; \, \lambda_1 = 1 $$ | $$ \lambda_2 = -1; \, \lambda_1 = 1 $$ | $$ \lambda_2 = 1; \, \lambda_1 = -1 $$ | $$ \lambda_2 = -1; \, \lambda_1 = -1 $$ | ||
$$ \text{energy} $$ |
$$ E' = \lambda_1 E $$ |
$$ E $$ |
$$ E $$ |
$$ -E $$ |
$$ -E $$ |
$$ \text{momentum} $$ |
$$ \text{p}' = \lambda_2 \, \text{p} $$ |
$$ \text{p} $$ |
$$ -\text{p} $$ |
$$ \text{p} $$ |
$$ -\text{p} $$ |
$$ \text{passage} $$ |
$$ \text{f}\,' = \lambda_2 \, \lambda_1 \, \text{f} $$ |
$$ \text{f} $$ |
$$ -\text{f} $$ |
$$ -\text{f} $$ |
$$ \text{f} $$ |
$$ \text{spin} $$ |
$$ \text{s}' = \text{s} $$ |
$$ \text{s} $$ |
$$ \text{s} $$ |
$$ \text{s} $$ |
$$ \text{s} $$ |
No transformation modifies the spin. \(\text{T}\)-symmetry is what makes a particle inverts its energy.
Here we provide the main excerpt of Souriau's book Structure of Dynamical Systems, Chapter 14 "A mechanistic description of elementary particles", pp. 189–193:
→ J.-M. Souriau: Inversions of space and time, pp. 189–193 ←
T-symmetry in Quantum Field Theory
Linear & unitary vs antilinear & antiunitary operators
Souriau's work presented above leads us to question the nature of the operator \(\text{T}\), which reverts time.
As we have shown, in dynamical group theory the operator \(\text{T}\) is real, and \(\text{T}\)-symmetry produces energy (and mass) inversion.
However, in quantum field theory (QFT), operators are complex. They can then be unitary or antiunitary, and linear or antilinear. Below, we show that the arbitrary choice of an operator \(\text{T}\) antilinear and antiunitary in QFT was made on the sole purpose to avoid negative energy particles, considered as impossible.
Indeed, Steven Weinberg wrote, in the "bible" book The Quantum Theory of Fields Vol. 1 (Cambridge University Press, 1995), chapter 2 "Relativistic Quantum Mechanics", section 2.6 "Space Inversion and Time-Reversal", pp. 75–76 (emphasis added): 9
At this point we have not yet decided whether \(\text{P}\) and \(\text{T}\) are linear and unitary or antilinear and antiunitary.
The decision is an easy one. Setting \(\rho = 0\) in Eq. (2.6.4) gives
$$ \text{P} \, i \, H \, \text{P}^{-1} \, = \, i \, H \text{,}$$
where \(H \equiv P^0\) is the energy operator. If \(\text{P}\) were antiunitary and antilinear then it would anticommute with \(i\), so \(\text{P} H \text{P}^{-1}=-H\). But then for any state \(\Psi\) of energy \(E > 0\), there would have to be another state \(\text{P}^{-1}\Psi\) of energy \(−E < 0\). There are no states of negative energy (energy less than that of the vacuum), so we are forced to choose the other alternative: \(\text{P}\) is linear and unitary, and commutes rather than anticommutes with \(\text{H}\).
On the other hand, setting \(\rho = 0\) in Eq. (2.6.6) yields
$$ \text{T} \, i \, H \, \text{T}^{-1} \, = \, -i \, H \text{.}$$
If we supposed that \(\text{T}\) is linear and unitary then we could simply cancel the \(i\)s, and find \(\text{T} H \text{T}^{-1}=-H\), with the again disastrous conclusion that for any state \(\Psi\) of energy \(E\), there is another state \(\text{T}^{-1}\Psi\) of energy \(−E\). To avoid this, we are forced here to conclude that \(\text{T}\) is antilinear and antiunitary.
Original excerpt available here:
→ S. Weinberg: Space Inversion and Time-Reversal, pp. 74–76 ←
Although British physicist Paul Dirac literally interpreted his discovery, in 1930, of negative-energy quantum states from his own equations as the Dirac sea, an infinitely deep sea of particles with negative energy, the modern interpretation from quantum field theory is that negative energy states are forbidden, as the zero-point field of the quantum vacuum represents a ground state of lowest possible energy, so energy states below the zero value could not exist. Indeed, the probability of existence of energy states in quantum mechanics implies the ratio \(E/m\). Therefore, if the energy is negative, that probability would be negative.
But it is a biased explanation, as if the energy is negative, so is the mass (which would also emit negative energy photons)… hence the probability remains positive. Positive energy and negative energy states would coexist in two separate worlds with increasing energy potential from both sides of a common ground state of lowest possible energy.
Fortunately, we've just shown that the foundations of quantum mechanics do in fact allow such negative energy states arbitrary dismissed from quantum field theory but predicted by the Janus model. 10
A Fifth Dimension
Geometric quantization
of the electric charge
Let us return to Souriau's work in geometric quantization and dynamical systems theory. The motion of the relativistic material point (symmetry, rotation, translation through time) is managed by the Poincaré group, which is a "dynamical group". It contains a subgroup, the Lorentz group, which acts upon points, for example in a 4D spacetime \([t, x, y, z]\), that are events.
In 1958, adding a compact (microscopic) 5th space dimension \(\zeta\) folded on itself as a fiber bundle in a five-dimensionnal relativistic theory (allowing to retrieve the Jordan-Thiry and Kaluza-Klein 5D theories, or Maxwell and Einstein 4D theories, as approximations), Souriau created a new five-dimensional Lorentz group describing events in a 5D spacetime \([x, y, z, t, \zeta]\). With this extended Lorentz group, he gave the first geometric interpretation of the matter-antimatter duality. When the additional dimension \(\zeta\) is defined modulo \(2\pi\), the electric charge \(e\) is quantized.

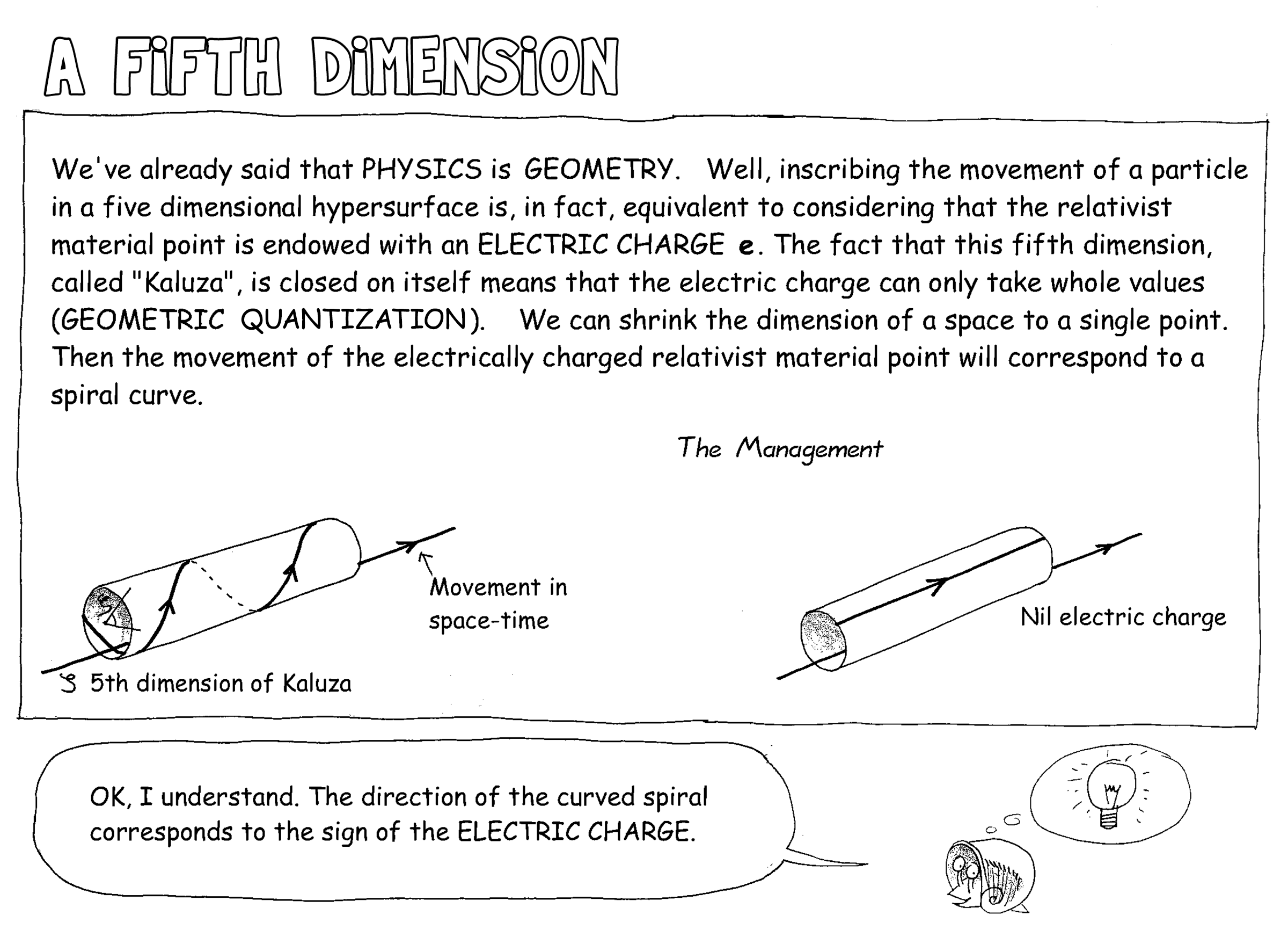
The Kaluza space, hyperbolic Riemannian of signature \((+----)\), has a 5×5 Gram matrix:
$$ \Gamma = \begin{vmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & -1 \end{vmatrix} \, = \, \begin{vmatrix} \text{G} & 0 \\ 0 & -1 \end{vmatrix} \qquad {\small \text{where}} \qquad \text{G} \, = \, \begin{vmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{vmatrix} $$
The metric of the Kaluza space is:
$$ d\Sigma^2 = dt^2 - dx^2 - dy^2 - \ dz^2 - d\zeta^2 $$
$$ r = \begin{bmatrix} x \\ y \\ z \end{bmatrix} \qquad \xi = \begin{bmatrix} t \\ x \\ y \\ z \end{bmatrix} = \begin{bmatrix} t \\ r \end{bmatrix} \qquad \Omega = \begin{bmatrix} t \\ x \\ y \\ z \\ \zeta \end{bmatrix} = \begin{bmatrix} \xi \\ \zeta \end{bmatrix} = \begin{bmatrix} t \\ r \\ \zeta \end{bmatrix} $$
$$ d\Sigma^2 \, = \, {}^\text{t}\kern{-2pt}d\Omega \; \Gamma \; d\Omega $$
If we look for the isometry group of this Kaluza space, we find a group with a matrix representation that looks very much like the one from a Poincaré group, but with an extra dimension:
$$ \begin{bmatrix} \Lambda & \Xi \\ 0 & 1 \end{bmatrix} \qquad {\small \text{with}} \qquad {}^\text{t}\kern{-2pt}\Lambda \, \Gamma \, \Lambda = \Gamma $$
The vector \( \Xi \) represents here a spacetime translation within five dimensions:
$$ \Xi = \begin{bmatrix} \Delta t \\ \Delta x \\ \Delta y \\ \Delta z \\ \Delta \zeta \end{bmatrix} $$
This group acts on the points of the 5D spacetime, the space of trajectories:
$$ \begin{bmatrix} \Lambda & \Xi \\ 0 & 1 \end{bmatrix} \times \begin{bmatrix} \Omega \\ 1 \end{bmatrix} = \begin{bmatrix} \Lambda \Omega + \Xi \\ 1 \end{bmatrix} $$
Translations along the fifth dimension \(\zeta\) represent a subgroup of this group, whose matrix representation is (subgroup with 1 parameter):
$$ \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & \Delta \zeta \\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} t \\ x \\ y \\ z \\ \zeta \\ 1 \end{bmatrix} = \begin{bmatrix} t \\ x \\ y \\ z \\ \zeta+\Delta\zeta \\ 1 \end{bmatrix} $$
And Noether's theorem says that a new scalar will be invariant under the action of this subgroup, and this scalar is

The Kaluza group is built from a group \(\Lambda\). The Lorentz group is one of its subgroups, whose element is:
$$ g = \begin{pmatrix} \text{L} & 0 \\ 0 & 1 \end{pmatrix} $$
Here is another subgroup of the Kaluza group:
$$ \begin{bmatrix} \text{L} & 0 & 0\\ 0 & \lambda & 0 \\ 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} \xi \\ \zeta \\ 1 \end{bmatrix} = \begin{bmatrix} \text{L}\xi \\ \lambda\zeta \\ 1 \end{bmatrix} \qquad {\small \text{with}} \qquad \lambda = \pm 1 $$
The element \((\lambda=-1)\) of this group inverts the fifth dimension. Taking the previous sketch of such compact dimension closed on itself:
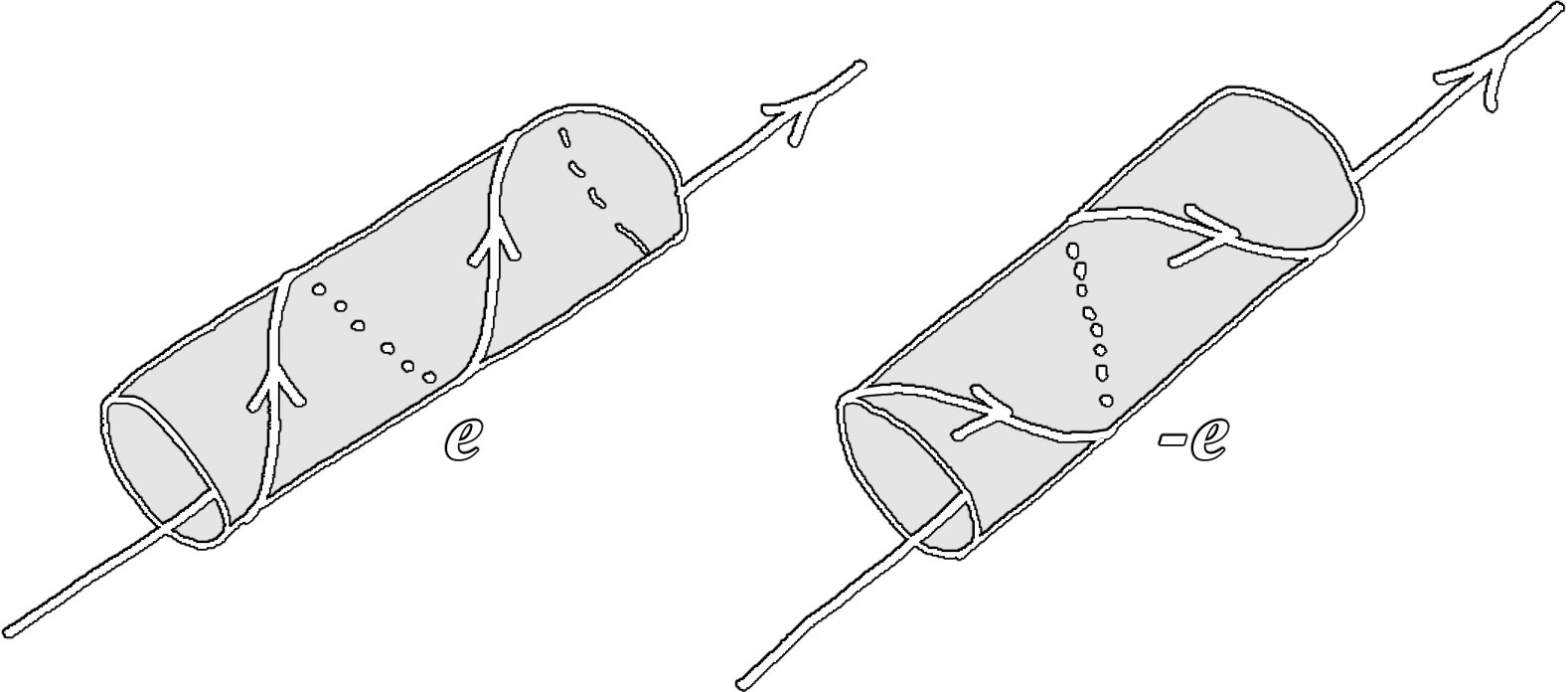 |
The winding direction of the particle's motion is reversed. Souriau shows that this implies the inversion of the electric charge, or \(\text{C}\)-symmetry. |
This illustrated geometric interpretation and the short explanation with groups correspond to a larger mathematical work published by Souriau only in French in the early 1960s, which left the worldwide scientific community largely unaware of it. Yet these papers are available online for free.
11
12
13
14
Related papers making this work more explicit in English according to the framework of the Janus cosmological model are also available.
15
16
17
18
It must be said here that the electric charge alone cannot be a complete geometrical definition of antimatter with charge conjugation, as particles own other quantum numbers, that can also be quantized with the same tools, but on which we won't expand further here. The purpose of this short presentation was to show the idea that antimatter depends of a type of motion in a higher dimensional space; and to give the interested reader the opportunity to consult the referenced literature.
References
1 Sakharov, A. D. (January 1967):
"Нарушение СР–инвариантности, С–асимметрия и барионная асимметрия Вселенной"
Pi'sma ZhÉTF (in Russian). 5 (1): 32–35.
Translated as:
Sakharov, A. D. (January 1967):
"Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe"
JETP Letters. 5 (1): 24–26.
Republished as:
Sakharov, A. D. (May 1991):
"Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe"
Soviet Physics Uspekhi. 34 (5): 392–393. doi:10.1070/PU1991v034n05ABEH002497.
2
Sakharov, A. D. (September 1980):
"Космологические модели Вселенной с поворотом стрелы времени"
Pi'sma ZhÉTF (in Russian). 79 (3): 689–693.
Translated as:
Sakharov, A. D. (September 1980):
"Cosmological models of the Universe with reversal of time's arrow"
JETP Letters. 52 (3): 349–351.
3
Sakharov, A. D. (October 1982):
"Многолистные модели Вселенной"
Pi'sma ZhÉTF (in Russian). 82 (3): 1233–1240.
Translated as:
Sakharov, A. D. (October 1982):
"Many-sheeted models of the Universe"
JETP. 56 (4): 705–709.
4 Sakharov, A. D. (7 December 1982): Collected Scientific Works. Marcel Dekker / CRC Press. ISBN 978-0824717148.
5 Sakharov, A. D. (1984): Œuvres scientifiques. Economica Anthropos. ISBN 978-2715710900.
6 Petit, J.-P. (23 May 1977):
"Univers jumeaux, énantiomorphes, à temps propres opposés"
[Enantiomorphic twin universes with opposite proper times]
Comptes rendus de l'Académie des Sciences (in French). Paris. 263: 1315–1318.
7 Petit, J.-P. (6 June 1977):
"Univers en interaction avec leurs images dans le miroir du temps"
[Universes interacting with their opposite time-arrow fold]
Comptes rendus de l'Académie des Sciences (in French). Paris: French Academy of Sciences. 284: 1413–1416.
8 Souriau, J.-M. (1970): "Description mécaniste des particules élémentaires : Inversions d’espace et de temps" in Structure des Systèmes Dynamiques, Dunod (1970).
Translated as:
Souriau, J.-M. (1997): "A mechanistic description of elementary particles: Inversions of space and time" in Structure of Dynamical Systems, Progress in Mathematics, Birkhäuser, pp. 189–193 (1997). ISBN 978-1-4612-6692-1. doi:10.1007/978-1-4612-0281-3_14.
9 Weinberg, S. (1995): "Relativistic Quantum Mechanics", in The Quantum Theory of Fields, Cambridge University Press, pp. 75–76 and p. 104 (1995). ISBN: 978-0521670531. doi:10.1017/CBO9781139644167.
10 Debergh, N.; Petit, J.-P.; D'Agostini, G. (November 2018):
"On evidence for negative energies and masses in the Dirac equation through a unitary time-reversal operator"
Journal of Physics Communications. 2 (11): 115012. doi:10.1088/2399-6528/aaedcc. arXiv:1809.05046.
11 Souriau, J.-M. (1958):
"Une axiomatique relativiste pour la microphysique"
[A relativistic axiomatic for microphysics]
Comptes rendus de l'Académie des Sciences (in French). Paris: French Academy of Sciences. 247: 1159–1562.
12 Souriau, J.-M. (1959):
"Conséquences physiques d’une théorie unitaire"
[Physical consequences of a unified theory]
Comptes rendus de l'Académie des Sciences (in French). Paris: French Academy of Sciences. 248: 1478–1480.
13 Souriau, J.-M. (1959):
"Relativité multidimensionnelle non stationnaire"
[Non-stationary multidimensional relativity],
International CNRS meetings: Relativistic theories of gravitation. pp. 293–297.
14 Souriau, J.-M. (1962): "Relativité à 5 dimensions" [5-dimensional Relativity], in Géométrie et Relativité [Geometry and Relativity]. Hermann Mesnil (in French). Republished by Jacques Gabay (2008). ISBN 978-2876473218.
15 Petit, J.-P.; Midy, P.; Landsheat, F. (June 2001):
"What twin matter could be made of", in Twin matter against dark matter
Marseille Cosmology Conference Where's the Matter? Tracing Dark and Bright Matter with the New Generation of Large Scale Surveys, Marseille, France. pp. 30–32.
16 Henry-Couannier, F.; d'Agostini, G.; Petit, J.-P. (February 2005):
"I- Matter, antimatter and geometry. II- The twin universe model: a solution to the problem of negative energy particles. III- The twin universe model plus electric charges and matter-antimatter symmetry"
arXiv:0712.0067.
17
Petit, J.-P.; D'Agostini, G. (2008)
"Five Dimensional bigravity. New topological description of the Universe".
arXiv:0805.1423.
18 Petit, J.-P. (January 2018):
"A Symplectic Cosmological Model"
Progress in Physics. 14 (1): 38–40.




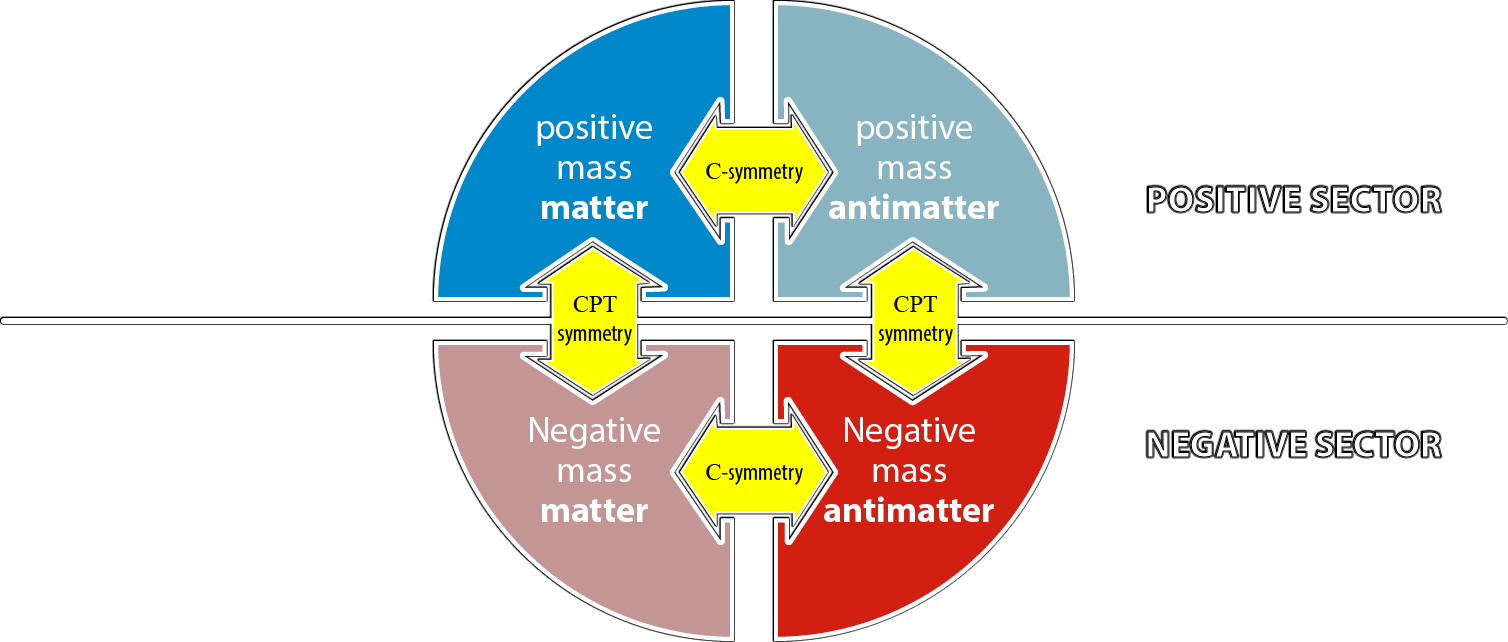
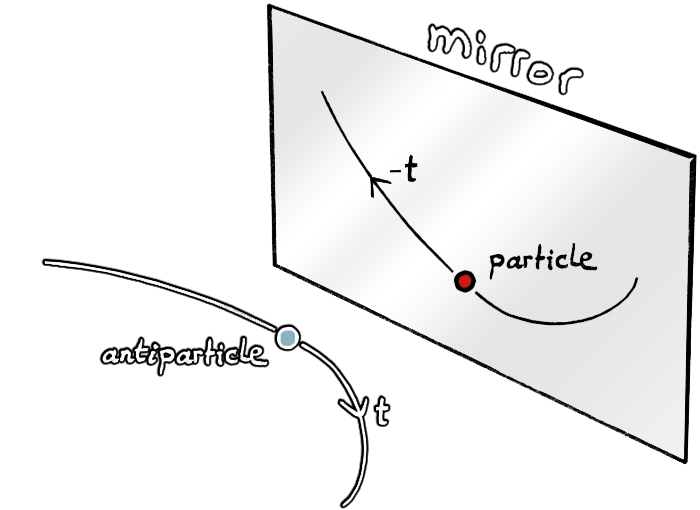 * According to great American physicist Richard Feynman, an antiparticle (\(\text{C}\)-symmetry) would be indistinguishable from the image in a mirror (\(\text{P}\)-symmetry) of its particle running backward in time (\(\text{T}\)-symmetry). This is related to the "\(\text{CPT}\) theorem", which claims that the \(\text{CPT}\) symmetry of a particle is the very same as that particle. But the \(\text{CPT}\) theorem is an axiom valid in a world where only positive energy states can exist. Since \(\text{T}\)-symmetry reverses the energy of a particle, the \(\text{CPT}\) theorem must be reconsidered.
* According to great American physicist Richard Feynman, an antiparticle (\(\text{C}\)-symmetry) would be indistinguishable from the image in a mirror (\(\text{P}\)-symmetry) of its particle running backward in time (\(\text{T}\)-symmetry). This is related to the "\(\text{CPT}\) theorem", which claims that the \(\text{CPT}\) symmetry of a particle is the very same as that particle. But the \(\text{CPT}\) theorem is an axiom valid in a world where only positive energy states can exist. Since \(\text{T}\)-symmetry reverses the energy of a particle, the \(\text{CPT}\) theorem must be reconsidered.
