The Einstein
Field Equations
Work with positive mass only
The classical Einstein field equations, which determine the geometry of spacetime (as a 4D hypersurface) in the presence of matter, can be written:
$$ R_{\mu\nu} - {1 \over 2} R \; g_{\mu\nu} \, = \, \chi \, T_{\mu\nu} $$
with a zero cosmological constant.
\( R_{\mu\nu} \) is the Ricci curvature tensor which expresses the degree to which space is curved with respect to flat Euclidean space. It is obtained from the contracted Riemann curvature tensor.
\( R \) is the Ricci scalar or scalar curvature, i.e. how much the volume of an object deviates from that in flat Euclidean space. It is the trace of the Ricci curvature tensor.
\( g_{\mu\nu} \) is the metric tensor or simply called the metric. It is how fundamental properties of spacetime (i.e. distance, volume, curvature, angle, time…) are calculated. It also separates the future from the past.
\( \chi \) is Einstein's constant which is a coupling constant directly proportional to Newton's gravitational constant \( G \).
\( T_{\mu\nu} \) is the stress–energy tensor, the cause of the disturbance of spacetime, i.e. the source of the gravitational field, due to the local presence of matter, radiation or non-gravitational force fields (like the electric field for example).
The metric \( g_{\mu\nu} \) secretes a family of geodesics. Note that test particles with a positive or a negative passive gravitational mass, as they follow the same geodesics, would behave the same way when embedded in a gravitational potential created by a large mass \( M \), for example in the Earth gravity.
Two coupled
field equations
How to reintroduce negative mass
Both positive and negative mass can coexist in the universe according to the Janus cosmological model, using two coupled field equations that naturally prevent the runaway paradox:
$$ R_{\mu\nu}^{(+)} - {1 \over 2} R^{(+)} g_{\mu\nu}^{(+)} = \chi {\Bigg[T_{\mu\nu}^{(+)} + \sqrt{g^{(-)} \over g^{(+)}}T_{\mu\nu}^{(-)}\Bigg]} $$
$$ R_{\mu\nu}^{(-)} - {1 \over 2} R^{(-)} g_{\mu\nu}^{(-)} = -\chi {\Bigg[ \sqrt{g^{(+)} \over g^{(-)}}T_{\mu\nu}^{(+)}+T_{\mu\nu}^{(-)}\Bigg]} $$
Spacetime according to Einstein is a 4D hypersurface with "a single side" (one metric \( g_{\mu\nu} \)). The 4D hypersurface now has "two sides", a frontside and a backside (two metrics):
The first metric \(g_{\mu\nu}^{(+)}\) refers to a family of geodesics with positive mass and positive energy particles, while the second metric \(g_{\mu\nu}^{(-)}\) refers to another, distinct family of geodesics with negative mass and negative energy particles.
It is important to note that negative mass particles emit negative energy photons that cannot be detected by optical instruments, because they follow null geodesics of the metric \(g_{\mu\nu}^{(-)}\) distinct from geodesics of our metric \(g_{\mu\nu}^{(+)}\). As positive energy species and negative energy species cannot see each other and evolve in two different families of geodesics, the two sides of spacetime they live in are respectively called the positive and the negative sector.
Although negative mass is invisible to us as it does not electromagnetically interact with positive mass matter, they do interact together through gravitation as they induce (opposite) curvatures in spacetime.
This is explained in detail in the Janus video #15:
You can watch the complete Janus video series available on YouTube.
New interaction laws
Newton & anti-Newton
Einstein's main idea with general relativity is that spacetime becomes curved by local concentration of mass, like the Earth or the Sun.
It is difficult to mentally picture a 3D deformation of space in a higher dimensional space. An easier representation of such a concept is often shown as a 2D didactic image of the rubber-sheet model: a planar (horizontal) rubber sheet is suspended in a uniform gravitational field normal to the sheet (vertical). A massive object like a bowling ball (star) or lead marbles (planets) put on this rubber sheet (or wire mesh) locally deforms it. This introduces Einstein's idea that mass distorts spacetime.
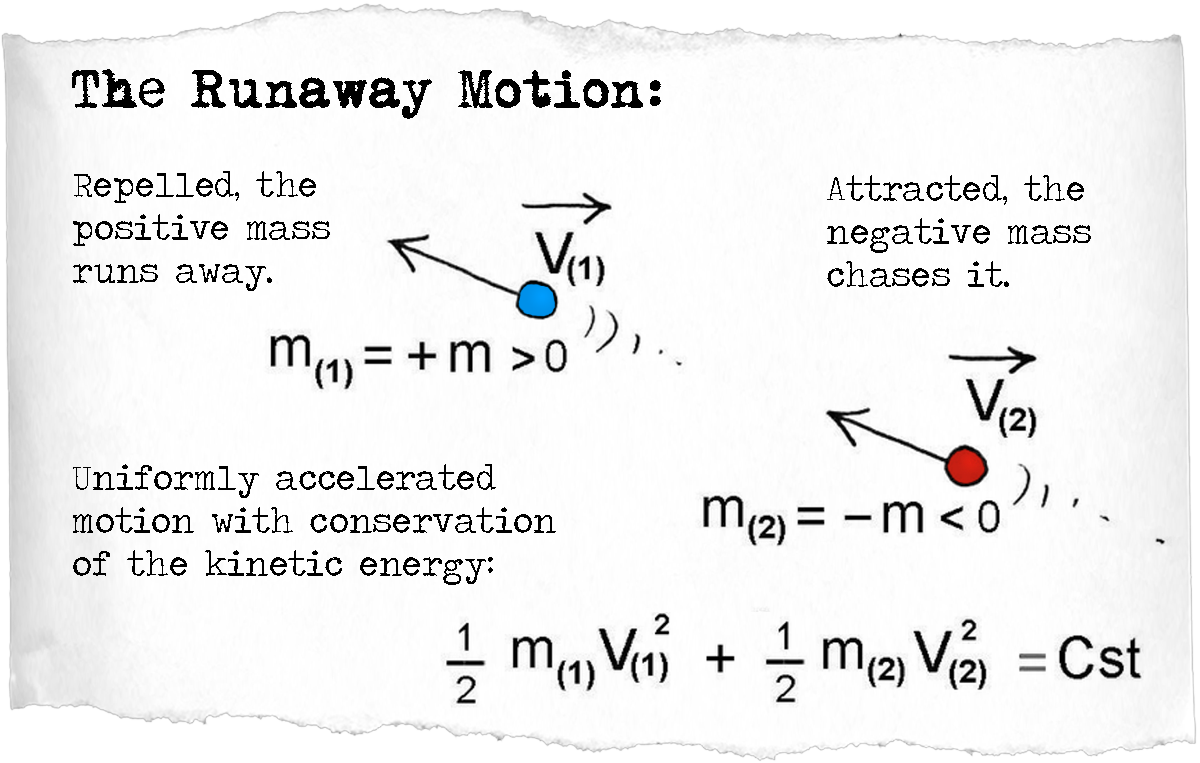
Positive mass (in blue in the image below) induces a gravitational potential the shape of a gravity well where other masses fall into: that is why matter is always gravitationnaly attractive. Classically in general relativity, hypothetical "exotic matter" made of negative mass (red) would conversely trigger an opposite gravitational potential in spacetime, the shape of a gravity hill. Such a negative gravitational potential would repulse any other mass around, including other negative masses.

Newtonian approximation
in general relativity
General relativity reduces to Newtonian gravity in the limit of small gravitational potential and low velocities with respect to the speed of light. So that locally, Newton's law of universal gravitation can be found using the Newtonian approximation of the Einstein field equations.
The interaction laws between positive and negative masses are then:

| Positive mass attracts positive mass |
Positive mass moves away from negative mass which chases it |
Negative mass repels negative mass |
Which can be summed up by "positive mass attracts everything" and "negative mass repels everything".
The figure in the middle illustrates the runaway motion: the positive mass moves away from the antigravitational potential of the negative mass, while the negative mass falls into the gravitational well of the positive mass and chases it. The couple then indefinitely accelerates, while its total energy stays constant, because the kinetic energy associated with the negative mass is negative! This gives rise to an inextricable paradox, which make astrophysicists and cosmologists think that negative mass could not really exist, as such very noticiable yet unphysical behavior is not observed in the universe.
Newtonian approximation
in the Janus model
The Janus model on the contrary implies two sides of the same coin. The universe can be assimilated to a single 4D hypersurface, which would have a frontside and a backside.
The motion of positive mass particles and the motion of negative mass particles do not occur on the same "side", or sector. Each species evolves along its own family of geodesics, in its own metric. Negative mass is among us, but invisible to us, being located "on the other side of the sheet", in its own "negative sector":

You may notice in the image above that the point of view of the gravity "well" vs "hill" has become opposite according from which side you are looking at: from a hypothetical observer made of negative mass located in the "other side" it is the Earth that would be invisible and felt as an "anomalous negative mass".
In the Janus model, negative mass is therefore not an intrinsic feature of such "exotic matter", but stem from topology; it is purely
Starting from the system of two coupled field equations of the Janus model, the Newtonian approximation gives new interaction laws (still proportionnal to 1/\(r^2\)) that differ from the classical Newtonian approximation calculated after the single field equation of general relativity:

| Positive mass attracts positive mass |
Positive mass and negative mass repel each other |
Negative mass attracts negative mass |
We see that:
- • Particles with mass of same signs mutually attract through Newton's law.
- • Particles with mass of opposite signs mutually repel through "anti-Newton's law".
The runaway paradox disappears: the Janus cosmological model finally enables the introduction of negative mass in cosmology. Moreover, accretion of negative mass particles in lumps of negative mass matter, through the Jean instability, is now possible as negative mass particles don't repulse themselves.
A new Einsteinian approximation
The system of two coupled field equations of the Janus model reduces to the Einstein field equations of general relativity for regions of spacetime where positive mass density largely dominates, i.e. where almost all negative mass has been repelled away by local concentration of positive mass matter, e.g. on Earth or in the solar system.
Therefore, the Janus cosmological model fits with local relativistic observations and measurements.
Positive & negative curvatures
Geodesics: The shortest path
The type and amount of curvature in spacetime is commonly showed with 2D surfaces embedded in our 3D world, on which a triangle is drawn:
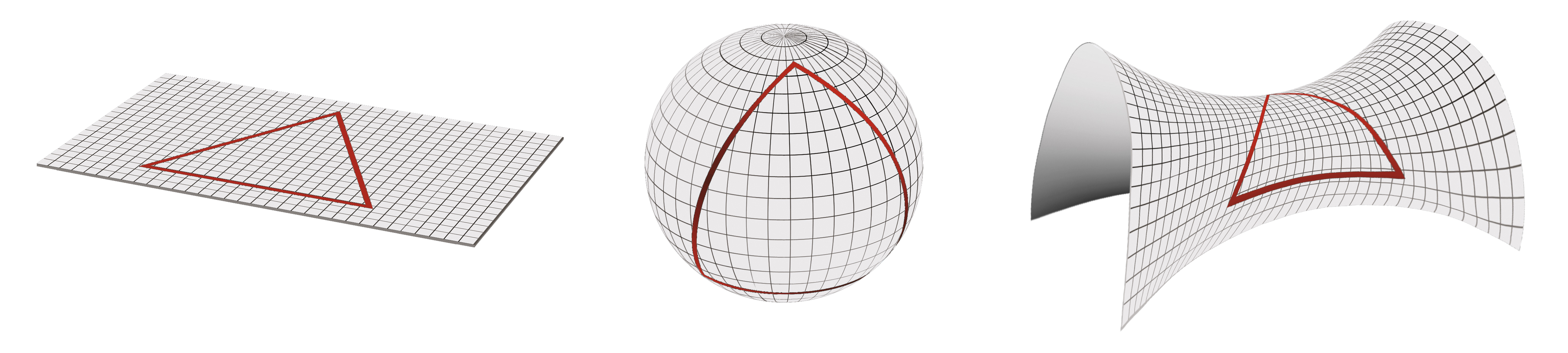
| EUCLIDEAN GEOMETRY (e.g. a flat sheet of paper) Zero-curvature The sum of angles of a triangle equals 180° |
SPHERICAL GEOMETRY (e.g. a ball) Positive curvature The sum of angles of a triangle is greater than 180° |
HYPERBOLIC GEOMETRY (e.g. a horse saddle) Negative curvature The sum of angles of a triangle is less than 180° |
The red lines drawing the triangles are the geodesics of the surface. A geodesic is the shortest path between two points in space. In a flat Euclidean space, this path is simply a straight line. On curved surfaces above (positive or negative) a geodesic can be drawn using a rope or an elastic drawn tight between two points on that surface.
Note that a "flat" Euclidean space, i.e. a space with zero curvature, is not necessarily a flat plane… The sheet above could be bent several times, for example like a corrugated iron sheet, its curvature will still be zero everywhere: geodesics traced ont its surface won't change. Same thing for closed Euclidean surface like a cylinder or a cone: contrary to what one might think, they do not have any curvature. According to the Euclidean geometry, they can be considered as "flat"!
As it is not so intuitive, the best way to know if a surface is Euclidean (zero-curvature) or curved (positive or negative curvature) is to make it pass the wrapping test:


The wall of a cone is flat (zero curvature) but the cone has a point of concentrated curvature at the apex.
Note also that a cone is a 2D surface, but is drawn in our 3D space. Topologically, we say that a cone is an embedding of a 2D surface in a 3D space.
In absence of matter, space if flat (Euclidean geometry). But the presence of some matter, locally, distorts spacetime. Matter induces a certain amount of positive curvature, proportional to the amount of mass. This is the essence of general relativity.
Posicone vs Negacone
In 2D, the amount of space curvature due to the presence of some mass can justly be represented by a cone, the mass being located at the apex. In reality, no mass is concentrated in a single point of space, it has a certain spatial extension. So it is best represented as a spherical cap (which contains a certain amount of curvature over its surface) joined to an empty flat space made of a truncated cone (an Euclidean surface). We then obtain a blunted cone:
Photons propagate in spacetime along its geodesics. When rays of light from Mercury appear to bend around the Sun (as observed for the first time by Sir Arthur Eddington during the 1919 Solar eclipse, corroborating Einstein's prediction from his theory of general relativity), they actually follow straight lines of spacetime, i.e. its geodesics. The apparent bending of light is therefore just an illusion, an "image projected on the wall of Plato's cave", as we are not able to directly see the deformation of spacetime produced by a three-dimensional object embedded in a higher-dimensional space. But we can draw it with less dimensions (using 2D surfaces), so we can understand what is going on:
We feel our world as if it was Euclidean, so we only see it as the "flat sheet". Therefore we see light rays bend around the Sun, as a curved path in a flat world. But this is an interpretation. In reality, light rays follow the "straight paths" of geodesics in a curved space.
Then, what about negative mass? Should we represent it with a cone put upside down, like an ice-cream cornet? No, because geodesics traced inside of a cone are exactly the same as on the outside: the spherical cap at the apex of a truncated cone has the same positive curvature whether it is measured "outside" or "inside": we call this object a posicone.
To represent negative mass, we have to draw a "special cone with negative curvature", i.e. a negacone. Such negacone has a hyperbolic geometry like the horse saddle above:
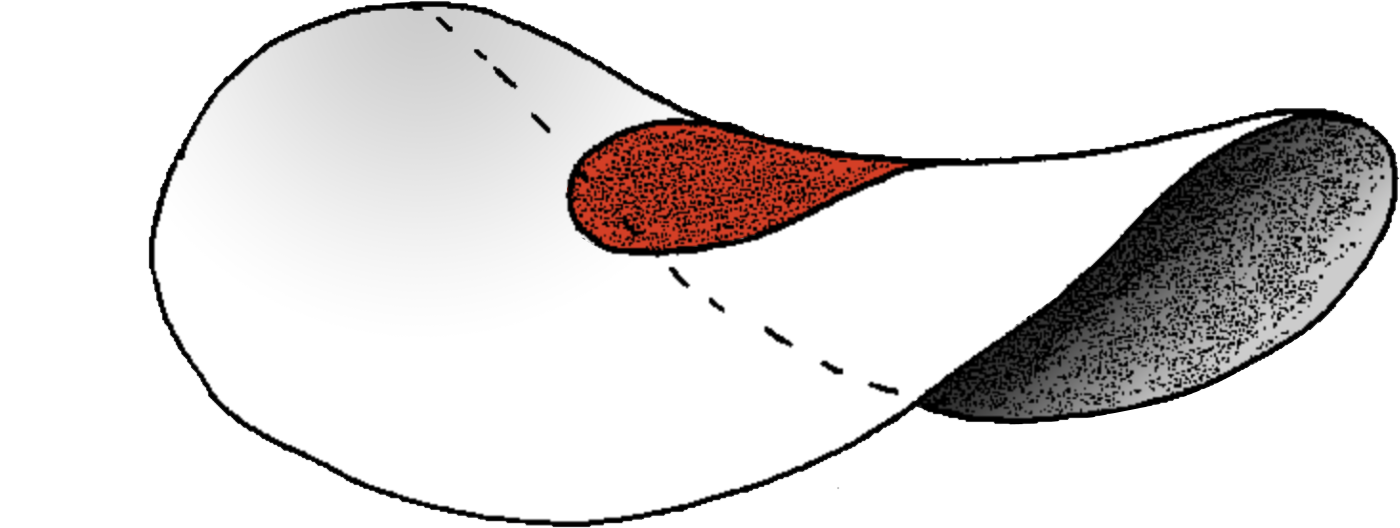
We also call such negacone a negachip, as its shape is exactly that of a Pringles© snack chip… Think about the quantity of negative curvature you swallow the next time you eat some of them!
Using posicones and negacones to represent positive and negative masses in spacetime is better than the rubber-sheet model presented in the previous section, because it actually shows the amount of curvature induced by positive and negative masses, how they distort spacetime differently and how geodesics take different paths.
As a consequence rays of light, which always follow geodesics, appear to bend differently around a positive mass (acting as a convergent lens) or around a negative mass (acting as a divergent lens):
![]()
Hence negative mass induces a negative gravitational lensing effect.
This is exposed in the Janus video #20, where Dr Petit explains that the current map of dark matter in the universe is done considering it has a positive mass, so the classical mapping is made after the arbitrary hypothesis that it induces a weak positive gravitational lensing effect distorting the image of faraway galaxies, like a converging lens. But a different map would be obtained with the hypothesis that dark matter has actually a negative mass, inducing a negative (divergent) lensing effect on the same images of galaxies. Such a map would directly test the Janus model and would falsify the theory, as it predicts that the resulting negative mass is essentially concentrated in the middle of the giant cosmic voids, around which galaxies are distributed in filaments and clusters in the very large-scale structure of the universe.
Conjugate curvatures
& the concept of
apparent mass:
One mass, two curvatures
Conjugate curvatures are the two opposite curvatures induced in spacetime by the presence of a single massive object, as measured according to each metric.
According to general relativity, spacetime is a 4D hypersurface. But as the classical Einstein field equations involve only one metric tensor, all matter belongs to one side of the 4D hypersurface, to a single metric, whatever its mass is positive or negative.
The system of two coupled field equations of the Janus model involves a 4D hypersurface with two sides, each type of mass belonging to its own metric. What is important to note however, is that the two field equations are coupled, i.e. a mass always creates a positive curvature in spacetime according to its own metric (where the mass appears visible), and it also always induces a negative curvature in the conjugate metric (where the mass appears invisible).

In this figure, a large mass (blue) belonging to the positive sector creates a positive curvature there. As a consequence, it produces a positive gravitational lensing effect on the image of a distant little positive mass \( m^{(+)} \), making photons of positive energy \( \varphi^{(+)} \) converging around the large mass. This large positive mass induces on the contrary a negative curvature in the negative sector. Hence, although being invisible, its apparent mass in the negative sector is felt as if it was negative. |
Opposite situation here: a large mass (red) belongs this time to the negative sector. There, it creates a positive curvature (not a negative one!). Such a mass being in the negative sector, we don't see it, but we feel its induced curvature in our sector, which is negative. We conclude that its apparent mass is negative. Indeed, il produces a negative gravitational lensing effect on the image of a distant little mass \( m^{(+)} \), making photons of positive energy \( \varphi^{(+)} \) diverging around the invisible but apparent large negative mass. |
You see in the two figures above that "negative mass" is not an intrinsic feature of some exotic matter. It is nothing but the (anti)gravitational effect produced by any mass, when it is felt from the opposite sector. According to an observer measuring such mass in the same sector where it lays in, that mass always appears positive.
This introduces the concept of apparent gravitational mass. Fundamentally, a mass is not "positive" or "negative": it is both! Its sign depends on "which side" we are measuring that mass. It is therefore a purely relative concept. Same thing for the "positive" and "negative" sectors: we call our sector the "positive" one simply because it is the one we live in, and we have to name both. But this is only a sign convention.
In the next page about \(\text{CPT}\) symmetry & antimatter, discover the direct link between time reversal and energy and mass inversion.